Géométrie (suite)
Du zonaède au Zome

Le zonaèdre est un objet mathématique abstrait, le zome est un zonaèdre construit. Géométriquement, il reste un zonaèdre ou une partie de zonaèdre.

Les zomes sont gouvernés par un paramètre essentiel, le nombre d'ordre N. Mais il existe des différérences entre les zomes selon que leur nombre N soit pair ou impair.

Les zomes ont un équateur. Pour les zomes pairs (comme ce zome 8), l'équateur est un plan de symétrie qui se situe au niveau de rang n = N / 2. Il partage le zome en deux moités identiques symétriques par rapport à l'équateur. La couronne entre les niveaux N/2 - 1 et N/2 + 1 porte des losanges verticaux.
   Les zomes d'ordre impair (comme ce zome 7) possèdent un équateur qui ne passe pas par des sommets. Il se situe entre les niveaux (N-1)/2 et (N+1)/2. Ce n'est pas un plan de symétrie sinon qu'une coupure à ce niveau présente une moitié basse indentique à la moitié haute inversée. Elles seraient symétriques à condition de faire subir à à la seconde une rotation autour de l'axe d'un angle i / 2, (i étant l'angle de révolution de 360° / N).
Ces zomes impairs n'ont pas de losanges verticaux avec (N-1)/2 couronnes saillantes et autant de couronnes rentrantes..

Coupes
      Pour une raison de stabilité, le zonaèdre complet va être coupé selon un plan horizontal pour faire reposer le zome sur un sol ou support horizontal, une dalle ou une plateforme sur pilotis. Il est logique de situer le plan de coupe à un niveau portant des sommets.
       Pour les zomes pairs, la coupure peut se situer à l'équateur ou à un niveau sous l'équateur. Dans le premier cas, les triangles verticaux, moitié des losanges de la couronne centrale, peuvent être prolongés par des murs rectangulaires verticaux de hauteur choisie par le constructeur. Dans le second cas, les pointes basses des losanges verticaux seront réunies pour former des triangles rentrants et un périmètre réduit de N côtés.
       Pour les zomes impairs, on conservera les (N-1)/2 couronnes saillantes au-dessus de l'équateur. On pourra les prolonger par 2N facettes verticales et trapézoïdales reposant sur le sol par un polygone de 2N côtés. Ou bien en reliant les pointes basses de la couronne du bas, on crée N triangles rentrants, reposant sur le sol en formant un polygone de N côtés

zomes coupés sous l'équateur ou coupés à l'équateur

Zome 6 reposant sur des triangles ou sur des murs zome 5 reposant sur des triangles ou sur des murs
18 losanges, 6 triangles '(demi-losanges) 12 losanges,6 triangles et 6 murs 10 losangrs (2 couronnes) et 5 triangles rentrants 10 losanges et 10 murs verticaux

Zome 6

EXTENSIONS
Ce sont des volumes que l'on rajoute pour agrandir l'espace habitable. Cela est plus aisé avec les zomes à N pair qui possèdent des facettes verticales.

Extension avec toit à une pente et toit à deux pentes Extensions avec une partie de zome ou par groupement avec un autre zome

ZONES

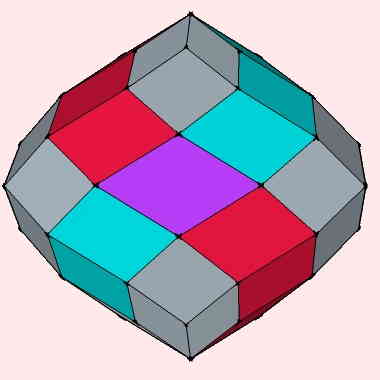
On nomme zone une bande brisée de losanges qui gardent une azête parallèle à une direction et qui ceinturent un zonaèdre.

Dans un zome ou zonaèdre polaire classique, il y a N zones. Les losanges sont créés par l'intersection de deux zones losange en violet au croisement des zones en rouge et en bleu) .
On peut étirer, ajouter ou supprimer une ou plusieurs zones, le nombre de losanges sera augmenté ou réduit. S'il se produit un croisement de 3 zones, cela créera un hexagone. 4 zones, un octogone, ...

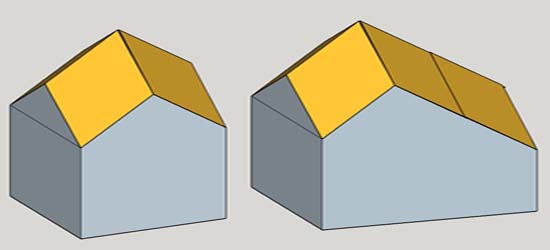Une zone étirée

Des ajouts de zones intéressants qui augmentent la surface des zomes en conservant la même hauteu (exemple zome 6)

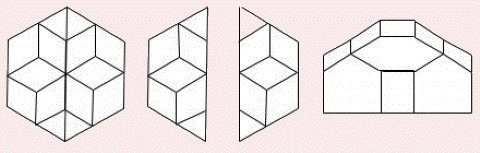
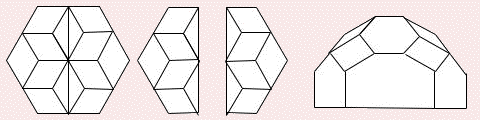
Un zome 6 coupé en deux moitiés et introduction d'une zone entre ces deux parties Deux possibilités de coupe donnant deux zonaèdres un peu différents

COMPRENDRE le zome
<