|
Un
peu de géométrie de
base (ça
ne fait pas de mal)
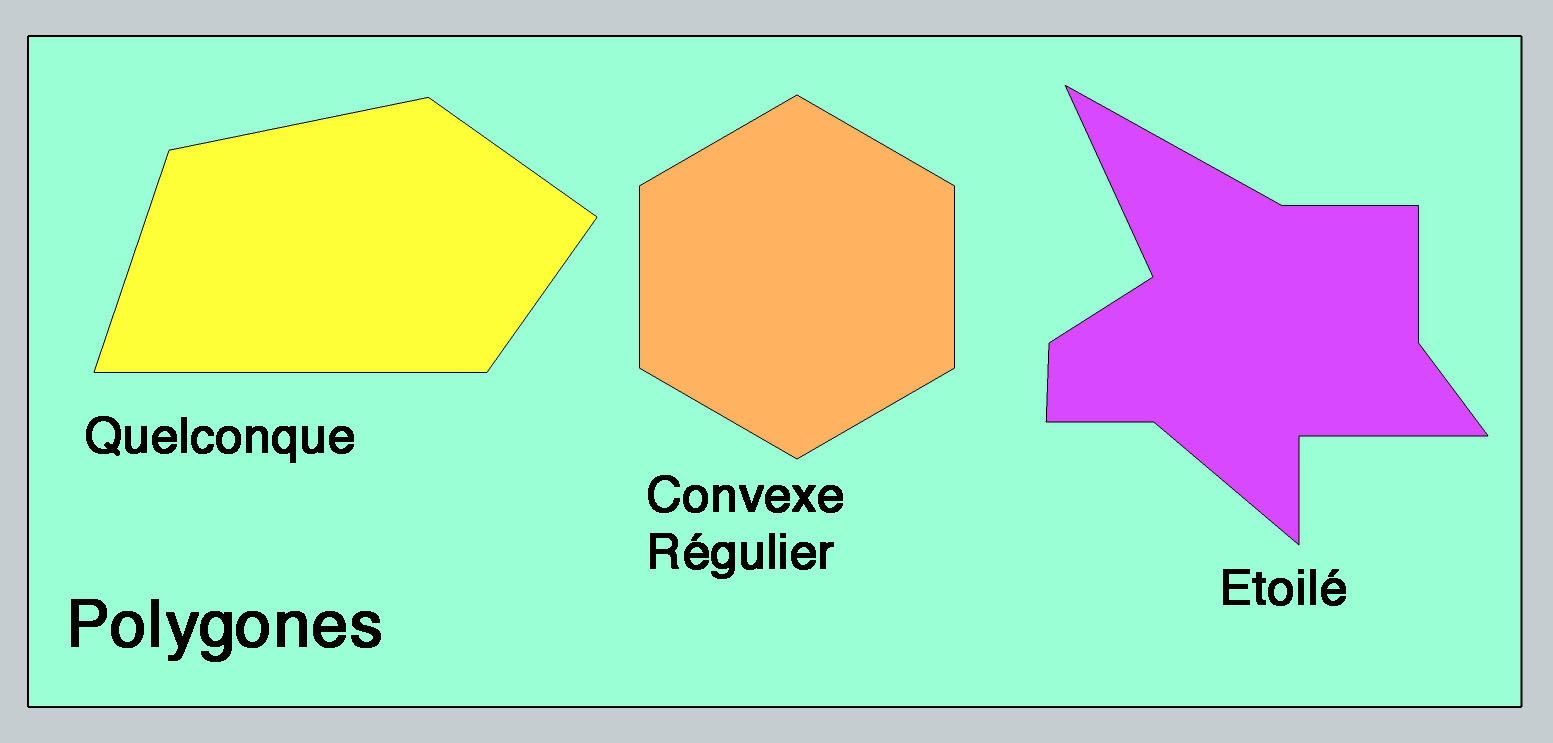
Les polygones sont des surfaces limitées
par des côtés qui les ceinturent.
Ils peuvent être quelconques ou
régulierssi avec tous les côtés de même longueur et des sommets à égale
distance d'un centre.
Convexes si tous les angles
intérieurs font moins de 180°. Sinon étoilés.
Les polyèdres sont des volumes entourés
entièrement de polygones
Les faces des polyèdres réguliers
sont identiques et sont des polygones réguliers
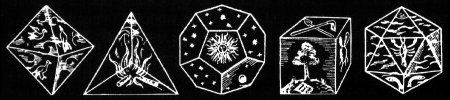
Les 5 polyèdres convexes et réguliers (polyèdres de Platon )
: octaèdre, tétraèdre, dodécaèdre,hexaèdre, icosaèdre
Les zonagones sont des polygones
réguliers ou non ayant des côtés égaux et parallèles 2 à 2. Ce qui
implique que ces zonagones aient un nombre pair de côtés, 4, 6,
8, ...
Les zonaèdres sont des polyèdres entièrement bordés
par des faces zonagonales
Les zonaèdres réguliers ont des faces polygonales
identiques
   
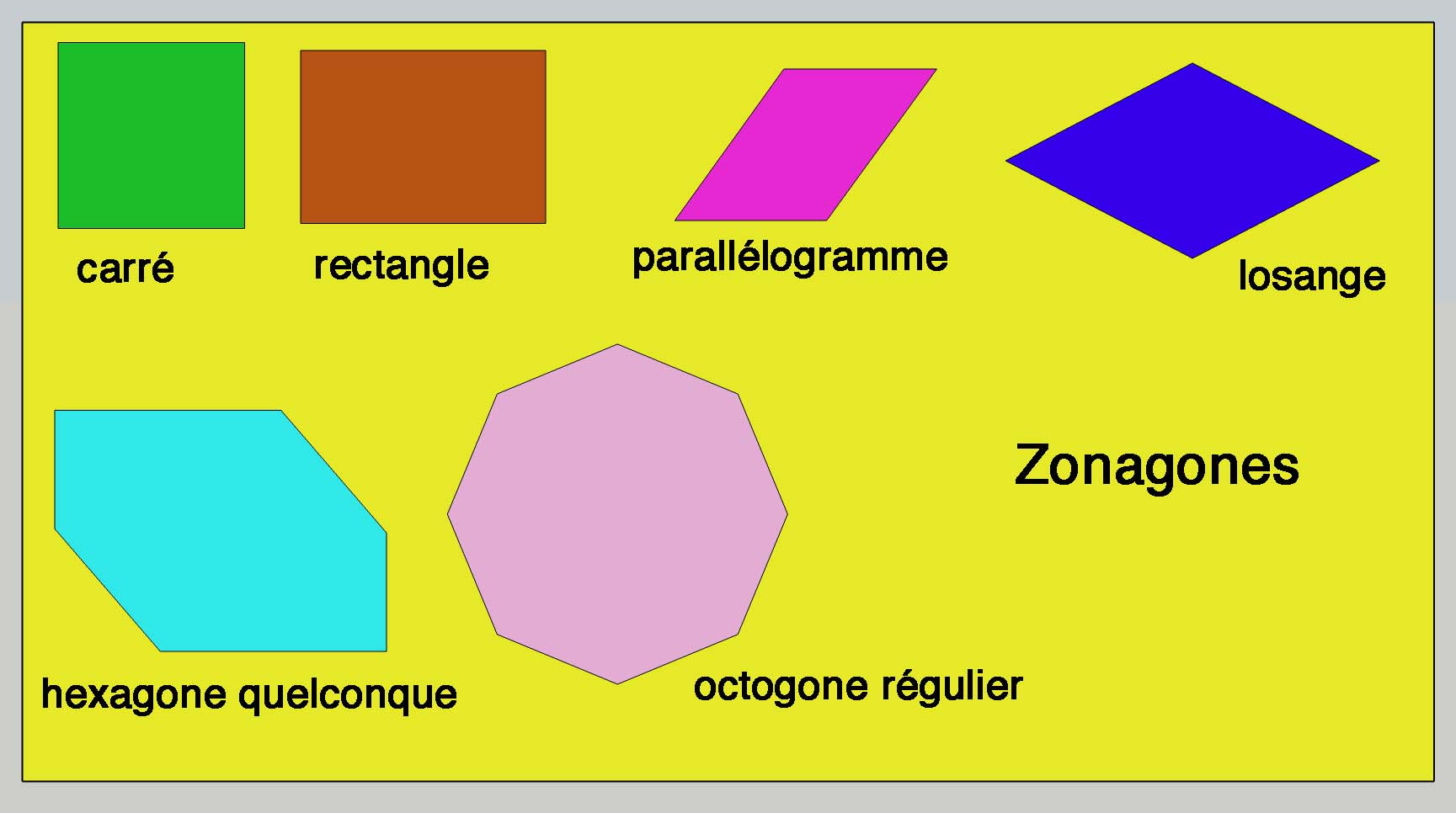
Zonaèdre régulier Deux zonaèdres quelconques sympatiques
Rhombizonaèdres
polaires de révolution (ou zonaèdres polaires)
Ce
sont des volumes
- composés
de losanges (rhombes)
- avec
2 sommets sur un axe fictif (les
pôles)
- possédant
une symétrie de
révolution par rapport à cet axe (se retrouvant
identique après la rotation d'un certain angle autour de cet
axe)
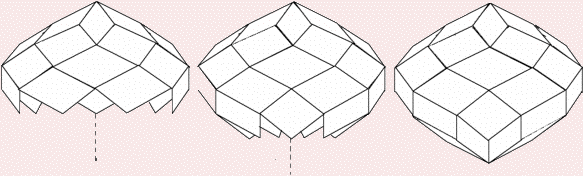
Création:
n arêtes
(ici 7) se réunissent en un point sur l'axe
en se répartissant
égalitairement
autour de cet axe fictif avec le même angle par rapport à l'axe.
Voilà le premier pôle et les première arêtes du zonaèdre.
Avec 2 arêtes voisines se crée le premier losange et les 6 autres au
même niveau.
Dans l'espace entre 2 losanges et avec ses arêtes basses, on crée une
autre couronne de losanges de niveau inférieur.
Et ainsi de suite.
Le zonaèdre gonfle mais près quelques processus
identiques, il atteint un volume maximum.commence à rétrécir;
et
finalement les arêtes convergent en un second pôle.
Ce processus de création est le même avec le même
résultat quel que soit le nombre d'arêtes de départ
(plus ou
moins rapidement selon le nombre de ces arêtes).
Composition
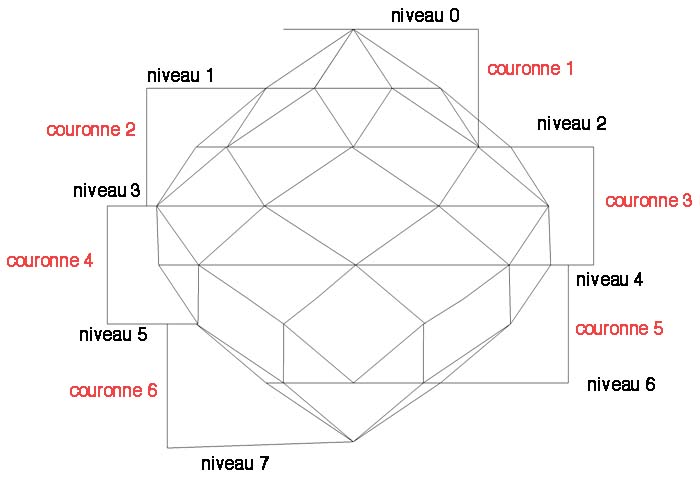
Ces
zonaèdres sont constitués de losanges qui se
regroupent en couronnes entourant l'axe. Dans une couronne, les
losanges sont
identiques. Les sommets sont situés sur des
plans
perpendiculaires à l'axe (les niveaux). La distance entre 2
niveaux successifs est constante, quelle que soit sa position dans le
zonaèdre.
3 paramètres
interviennent pour déterminer un
zonaèdre précis
De
lui dépend le nombre de couronne
= N - 1
Le
nombre de facettes par couronne
= N
Le
nombre total de facettes
= N *
(N - 1)
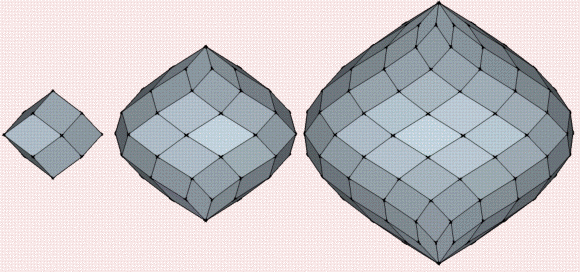 Zonaèdres
d'ordres 4, 8 et 12
F est
le nombre de forme, un second paramètre indépendant (nombre
entier, fractionnaire ou irrationnel, compris entre 0 et l'infini)
De
lui dépend la forme plus ou moins pointue du volume
Le
choix d'un nombre d'ordre et d'un nombre de forme va fixer la
forme du volume (la forme, mais pas sa dimension).
Plus ce nombre est petit, plus le zonaèdre des allongé,
plus ce nombre est grand, plus le zonaèdre est aplati.
Zonaèdres
de nombres de
forme de 2, 1 et 0,5
-
Un
paramètre
de taille (ou facteur d'échelle)
-
Si
la forme est fixée, le choix d'une seule dimension
(arête
ou diamètre, ou hauteur,...) va
déterminer la taille du volume et celle de chacun de ses
éléments
|
COMPRENDRE le zome
