Autoconstruction 1

Calculer et construire un zome

CONTENU

1- Page 1

Complément d'examen du zome
Définition et calculs d'un zome MODELE

Eléments du zome en PROJET
2- Page 2

Préparation au montage
La commande de bois
Le montage du zome PROJET

1- ZOME et Zomandala
On traitera des zomes polaires à axe vertical. Ils dépendent de deux paramètres de forme
- N, le nombre d'ordre qui détermine le nombre de couronnes et le nombre de losanges par couronne
- F le nombre de forme qui, avec la grandeur N choisie, fixe définitivement la forme du zome.

Figure précédente

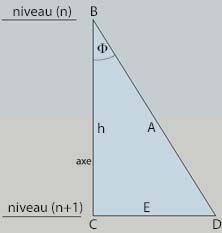
Toutes les arêtes des losanges du zome (comme A) ont la même longueur et forment le même angle avec l'axe vertical (ou toute parallèle à l'axe).

A débute sur un niveau (n) et aboutit sur le niveau (n+1) à une altitude plus basse de h.
L'extrémité inférieure s'éloigne de l'axe d'une grandeur E

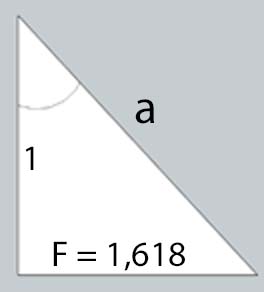
Le nombre de forme F est défini comme la tangente trigonométrique de l'angle F, (PHI) soit dans le triangle BCD

F = E / h

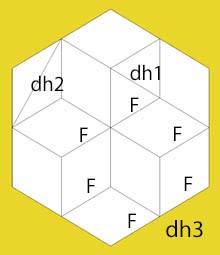
   Les losanges possèdent des diagonales obliques DO.
    Les secondes diagonales DH sont horizontale. Elles se projettent sans déformation sur un plan horizontal.
    De même pour les segments E horizontaux, projections sur ce plan des arêtes A du zome.

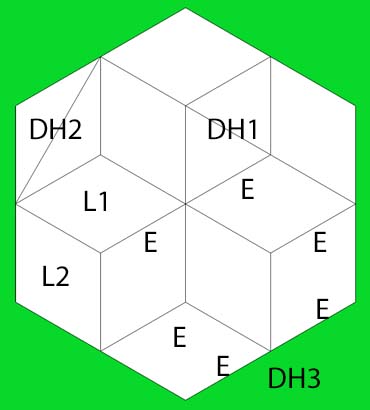
    On nommera zomandala la figure plane qui sera la projection de toutes les arêtes d'un zome sur un plan horizontal. Sa forme et sa complexité ne dépendront que du nombre d'ordre N (et pas de F).

Zomandala 6
Deux types de losanges sont visibles, L1 et L2
Avec leurs diagonales horizontales DH1 et DH2
Les côtés de l'hexagone se forment par deux E en prolongement:
ce sont les diagonales horizontales des losanges L3 verticaux du zome 6 source de ce zomandala

2- Définition et Calculs d'un modèle

On va jongler avec 3 ensembles

- Le PROJET
C'est le zome que l'on veut construire. Avec N et F choisis, il faut donner la dimension d'un élément.
Comme unités, on adoptera les mètres pour les longueurs ou les mètres carrés pour les surfaces.
Et comme exemple ce sera un zome 6 (N=6), de nombre de forme F=1,618 (le nombre d'Or) et d'une surface au sol de 20 m2.

- Le MODELE est un zome ayant exactement la même forme que le PROJET mais dont on impose la dimension d'un élément différent de sa surface.

Soit h = 1 mètre. C'est un zome ressemblant au PROJET mais de taille différente (plus ou moins grande ou petite)
L'introduction de ce MODELE va faciliter les calculs;

- Le ZOMANDALA du modèle.
Avec h=1, le nombre de forme F = E / h donne
E = F.
On remplacera E par F dans le zomandala précédent

Les places des losanges sont identiques dans le PROJET et dans le MODELE, losanges 1 (L1) liés au pôle supérieur et au centre dans le zomandala, et place des losanges suivants dans les couronnes suivantes.

On réservera les lettres en majuscules pour les éléments du PROJET, et celles en minuscules pour le zomandala (et éventuellement s'il le faut quelque chose de mixte pour le MODELE. Par exemple

- dh ou dH pour les diagonales horizontales du Zomandala et du MODELE (elles sont égales) et DH pour le PROJET

- a pour les arêtes du MODELE et A du PROJET

Calculs dans le MODELE- Méthode originale ZOMANDALA
En fait, elle autorise trois approches

       _ Méthode mathématique: la plus précise. Assez simple si l'on connait le théorème de Pythagore et quelques formules de trigonométrie.
       _ Méthode graphique: sans calculs mais des dessins. Précisoin suffisante si les dessins sont soigneux et de taille suffisante.
       _ Méthode sans calculs ni dessins. Prendre des données dans des tableaux, s'ils existent
Exemple en consultant ceux établis par la suite pour le Modele défini ci-dessus.

L'arête des losanges a = racine(F^2+1) a= 1,902 m On peut aussi obtenir ce résultat en dessinant cette figure et mesurant a	Losange 1	Losange 2	Losange 3	Zome 6 avec murs	Zome 6 rentrant
	Diagonale horizontale dh1= F=1,618	Diagonale horizontale dh2 = F*racine(3) = 2,802	Diagonale horizontale dh3 = 2F = 3,236	Surface à l'équateur 27,207	Surface à l'équateur 27,207
	Angle alpha dans le modèle 50,3°	Angle alpha 94,9°	Angle alpha 116,6°	Surface au sol 27,207	Surface au sol 20,405
	Diagonale oblique dans le zomandala 2,802	Diagonale oblique dans le zomandala 1,618	Diagonale oblique dans le zomandala 0	Hauteur au-dessus de l'équateur 3 m	Hauteur au-dessus du sol 4 m
	Surface (m2) dans le zomanda 2,267	Surface (m2) dans le zomandala 2,267	Surface (m2) dans le zomandala 0	Diamètre à l'équateur 6,472 m	Diamètre au sol 5,604 m
	Diagonale oblique dans le Modèle 3,443	Diagonale oblique dans le Modèle 2,573	Diagonale oblique dans le Modèle 2'	Côté de l'hexagone à l'équateur = 2*F = 3,236 m	Côté au sol de l'hexagone = dh2 = 2,802
	Pente par rapport à l'axe dans le Modèle 54,5°	Pente par rapport à l'axe dans le Modèle 39°	Pente par rapport à l'axe dans le Modèle 0°

Voilà le tableau relatif au MODELE du zome 6, de nombre de forme 1,618, avec h = 1 m. Etabli à partir des calculs mathématiques.
L'angle alpha est un des deux angles que l'on rencontre dans le type de losange indiqué:
plus précisément celui que l'on trouve dans les deux sommets opposés qui ne sont pas sur un même niveau
(les deux autres sommets opposés portent simplement un angle de 180° moins l'angle alpha).
La pente des losanges est celle de leurs diagonales obliques (pente minimum du losange par rapport à l'axe).

3- Valeurs des éléments du PROJET

    Le MODELE et le PROJET ayant la même forme, leurs angles sont identiques, en particulier:
leurs angles Alpha ainsi que les pentes de leurs losanges La surface à l'équateur ou au sol est aussi un héxagone.

R, facteur d'échelle (ou de proportionnalité)

Il s'agit du rapport entre la dimension d'un élément du PROJET er de celle du même élément du MODELE que l'on vient de calculer (tableau).
A une nuance près
R est le facteur d'échelle pour la comparaison de grandeurs de la première dimension, les longueurs.
Mais pour la comparaison des surfaces, deuxième dimension, ce rapport donnera rle carré de R
Pour le PROJET, on désire une surface de 20 m2.
Et en plus, on va tester deux situations: un zome avec murs de 20 m2 à l'équateur (et au sol), un zome rentrant de 20 m2 au sol.

Zome avec murs           20 / 27,207 = 0,735 = (R1) au carré               R1 = O,857
Il faudra donc multiplier toutes les longueurs calculées dans le MODELE par ce facteur d'échelle pour obtenir celles du PROJET
Les dimensions réelles des principaux éléments du zome sont données au mm ou au cm2 près.

Zome 6 avec murs

Longueur des arêtes

1,631

Diamètre à l'équateur

5,546

Côté de l'héxagone

2,773

Hauteur totale

2,571
+ DH

DH étant la hauteur des murs rectangulaires qu'il faudra choisir maintenant
en fonction de l'ésthétique de l'ensemble?
ou de la fonction du zome?
veux-on une mézzannine, un étage complet ? ...

Zome rentrant, coupure à 1 niveau sous l'équateur 20 / 20,405 = 0,98 = f(R2) au carré R2 = 0,990

Zome 6 rentrant coupé à 1 niveau sous l'équateur	Longueur des arêtes 1,883	Diamètre à l'équateur 6,407	Surface à l'équateur 26,93	Diamètre au sol 5,546	Surface au sol 20	Côté de l'haxgone au sol 2,774	Hauteur totale 3,96

-FERMER

suite Page 2